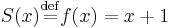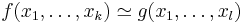μ-recursive function

In mathematical logic and computer science, the μ-recursive functions are a class of partial functions from natural numbers to natural numbers which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that can be computed by Turing machines. The μ-recursive functions are closely related to primitive recursive functions, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every μ-recursive function is a primitive recursive function — the most famous example is the Ackermann function.

Other equivalent classes of functions are the λ-recursive functions and the functions that can be computed by Markov algorithms.

The set of all recursive functions is known as R in computational complexity theory.

1 Definition
2 Equivalence with other models of computability
3 Normal form theorem
4 Symbolism
5 Examples
6 See also
7 External links
8 References

Definition

The μ-recursive functions (or partial μ-recursive functions) are partial functions that take finite tuples of natural numbers and return a single natural number. They are the smallest class of partial functions that includes the initial functions and is closed under composition, primitive recursion, and the μ operator.

The smallest class of functions including the initial functions and closed under composition and primitive recursion (i.e. without minimisation) is the class of primitive recursive functions. While all primitive recursive functions are total, this is not true of partial recursive functions; for example, the minimisation of the successor function is undefined. The set of total recursive functions is a subset of the partial recursive functions and is a superset of the primitive recursive functions; functions like the Ackermann function can be proven to be total recursive, and not primitive.

The first three functions are called the "initial" or "basic" functions: (In the following the subscripting is per Kleene (1952) p. 219. For more about some of the various symbolisms found in the literature see Symbolism below.)

Constant function: For each natural number 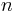$n\,$ and every $k\,$ :

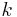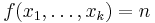$f(x_1,\ldots,x_k) = n\,$ .

Alternative definitions use compositions of the successor function and use a zero function, that always returns zero, in place of the constant function.
Successor function S:

$S(x) \stackrel{\mathrm{def}}{=} f(x) = x %2B 1\,$
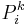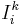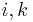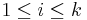Projection function $P_i^k$ (also called the Identity function $I_i^k$ ): For all natural numbers $i, k\,$ such that $1 \le i \le k$ :

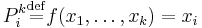$P_i^k \stackrel{\mathrm{def}}{=} f(x_1,\ldots,x_k) = x_i$ .
Composition operator 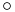$\circ\,$ (also called the substitution operator): Given an m-ary function $h(x_1,\ldots,x_m)\,$ and m k-ary functions $g_1(x_1,\ldots,x_k),\ldots,g_m(x_1,\ldots, x_k)$ :

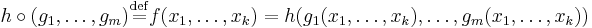$h \circ (g_1, \ldots, g_m) \stackrel{\mathrm{def}}{=} f(x_1,\ldots,x_k) = h(g_1(x_1,\ldots,x_k),\ldots,g_m(x_1,\ldots,x_k))\,$ .
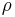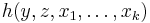Primitive recursion operator $\rho\,$ : Given the k-ary function $g(x_1,\ldots,x_k)\,$ and k+2 -ary function $h(y,z,x_1,\ldots,x_k)\,$ :

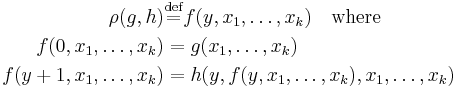$\begin{align} \rho(g, h) &\stackrel{\mathrm{def}}{=} f(y, x_1,\ldots, x_k) \quad {\rm where} \\ f(0,x_1,\ldots,x_k) &= g(x_1,\ldots,x_k) \\ f(y%2B1,x_1,\ldots,x_k) &= h(y,f(y,x_1,\ldots,x_k),x_1,\ldots,x_k)\,\end{align}$ .
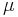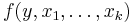Minimisation operator $\mu\,$ : Given a (k+1)-ary total function $f(y, x_1, \ldots, x_k)\,$ :

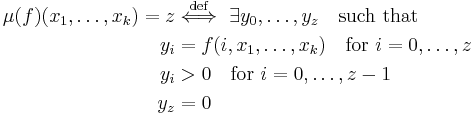
$\begin{align} \mu(f)(x_1, \ldots, x_k) = z &\stackrel{\mathrm{def}}{\iff}\ \exists y_0, \ldots, y_z \quad {\rm such\ that}\\ y_i &= f(i, x_1, \ldots, x_k) \quad {\rm for}\ i=0, \ldots, z \\ y_i &> 0 \quad{\rm for}\ i=0, \ldots, z-1 \\ y_z &= 0 \end{align}$

Intuitively, minimisation seeks--beginning the search from 0 and proceeding upwards--the smallest argument that causes the function to return zero; if there is no such argument, the search never terminates.

The strong equality operator 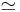$\simeq$ can be used to compare partial μ-recursive functions. This is defined for all partial functions f and g so that

$f(x_1,\ldots,x_k) \simeq g(x_1,\ldots,x_l)$

holds if and only if for any choice of arguments either both functions are defined and their values are equal or both functions are undefined.

Equivalence with other models of computability

In the equivalence of models of computability, a parallel is drawn between Turing machines which do not terminate for certain inputs and an undefined result for that input in the corresponding partial recursive function. The unbounded search operator is not definable by the rules of primitive recursion as those do not provide a mechanism for "infinite loops" (undefined values).

Normal form theorem

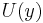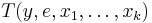A normal form theorem due to Kleene says that for each k there are primitive recursive functions $U(y)\!$ and $T(y,e,x_1,\ldots,x_k)\!$ such that for any μ-recursive function $f(x_1,\ldots,x_k)\!$ with k free variables there is an e such that

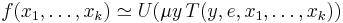$f(x_1,\ldots,x_k) \simeq U(\mu y\, T(y,e,x_1,\ldots,x_k))$ .

The number e is called an index or Gödel number for the function f. A consequence of this result is that any μ-recursive function can be defined using a single instance of the μ operator applied to a (total) primitive recursive function.

Minsky (1967) observes (as does Boolos-Burgess-Jeffrey (2002) pp. 94–95) that the U defined above is in essence the μ-recursive equivalent of the universal Turing machine:

To construct U is to write down the definition of a general-recursive function U(n, x) that correctly interprets the number n and computes the appropriate function of x. to construct U directly would involve essentially the same amount of effort, and essentially the same ideas, as we have invested in constructing the universal Turing machine. (italics in original, Minsky (1967) p. 189)

Symbolism

A number of different symbolisms are used in the literature. An advantage to using the symbolism is a derivation of a function by "nesting" of the operators one inside the other is easier to write in a compact form. In the following we will abbreviate the string of parameters x₁, ..., x_n as x:

Constant function: Kleene uses " C_qⁿ(x) = q " and Boolos-Burgess-Jeffry (2002) (B-B-J) use the abbreviation " const_n( x) = n ":

e.g. C₁₃⁷ ( r, s, t, u, v, w, x ) = 13

e.g. const₁₃ ( r, s, t, u, v, w, x ) = 13

Successor function: Kleene uses x' and S for "Successor". As "successor" is considered to be primitive, most texts use the apostrophe as follows:

S(a) = a +1 =_def a', where 1 =_def 0', 2 =_def 0 ' ', etc.

Identity function: Kleene (1952) uses " U_iⁿ " to indicate the identity function over the variables x_i; B-B-J use the identity function id_iⁿ over the variables x₁ to x_n:

U_iⁿ( x ) = id_iⁿ( x ) = x_i

e.g. U₃⁷ = id₃⁷ ( r, s, t, u, v, w, x ) = t

Composition (Substitution) operator: Kleene uses a bold-face S_n^m (not to be confused with his S for "successor" ! ). The superscript "m" refers to the m^th of function "f_m", whereas the subscript "n" refers to the n^th variable "x_n":

If we are given h( x )= g( f₁(x), ... , f_m(x) )

h(x) = S_mⁿ(g, f₁, ... , f_m )

In a similar manner, but without the sub- and superscripts, B-B-J write:

h(x')= Cn[g, f₁ ,..., f_m](x)

Primitive Recursion: Kleene uses the symbol " Rⁿ(base step, induction step) " where n indicates the number of variables, B-B-J use " Pr(base step, induction step)(x)". Given:

base step: h( 0, x )= f( x ), and
induction step: h( y+1, x ) = g( y, h(x,y),x )

Example: primitive recursion definition of a + b:

base step: f( 0, a ) = a = U₁¹(a)
induction step: f( b' , a ) = ( f ( b, a ) )' = g( b, f( b, a), a ) = g( b, c, a ) = c' = S(U₂³( b, c, a )

R² { U₁¹(a), S [ (U₂³( b, c, a ) ] }

Pr{ U₁¹(a), S[ (U₂³( b, c, a ) ] }

Example: Kleene gives an example of how to perform the recursive derivation of f(b, a) = b + a (notice reversal of variables a and b). He starting with 3 initial functions

S(a) = a'
U₁¹(a) = a
U₂³( b, c, a ) = c
g(b, c, a) = S(U₂³( b, c, a )) = c'
base step: h( 0, a ) = U₁¹(a)

induction step: h( b', a ) = g( b, h( b, a ), a )

He arrives at:

a+b = R²[ U₁¹, S₁³(S, U₂³) ]

Examples

External links

Stanford Encyclopedia of Philosophy entry

References

Stephen Kleene (1952) Introduction to Metamathematics. Walters-Noordhoff & North-Holland, with corrections (6th imprint 1971); Tenth impression 1991, ISBN 0-7204-2103-9.
Soare, R. Recursively enumerable sets and degrees. Springer-Verlag 1987.
Marvin L. Minsky (1967), Computation: Finite and Infinite Machines, Prentice-Hall, Inc. Englewood Cliffs, N.J.

On pages 210-215 Minsky shows how to create the μ-operator using the register machine model, thus demonstrating its equivalence to the general recursive functions.

George Boolos, John Burgess, Richard Jeffrey (2002), Computability and Logic: Fourth Edition, Cambridge University Press, Cambridge, UK. Cf pp. 70–71.